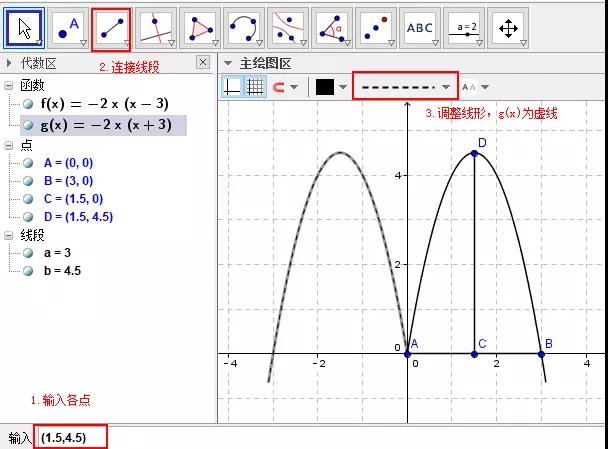
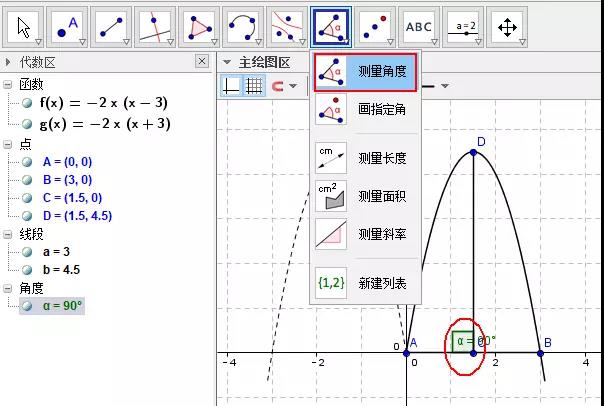
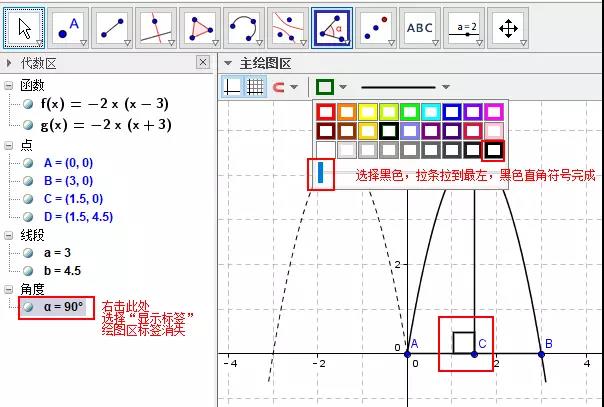
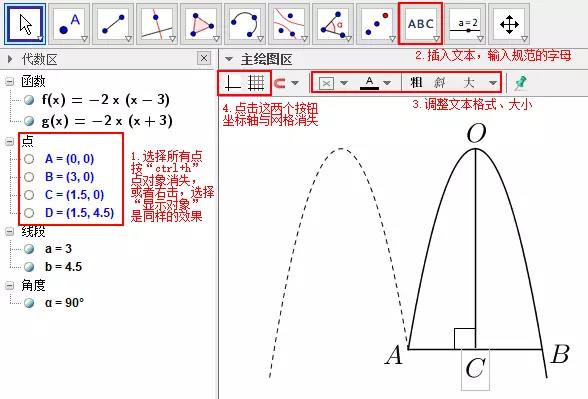
2008 年,中国教育学会主办的《中小学数学》(高中版)创刊。作为主编,在每一期杂志定稿后,我都会写一篇“编后漫笔”,这一习惯坚持至今。这些“千字文”都是针对数学教育教学中某一问题的一事一议,紧密结合教学实际,短小精悍,言简意赅,直言不讳,针砭时弊,答疑解惑,切实有用,每每能引发广大一线教师和注重课堂教学实践的数学教育研究者的共鸣,深受读者喜爱,许多读者希望将这些文章结集出版以便查阅。
同时,也有许多中学数学老师希望我把已发表的文章汇集成书正式出版,还有出版界的同行约稿,希望出版我的数学教育论文集。在朋友们的督促、鼓励和帮助下,经过近一年的努力,终于完成论文整理并编辑成书。
本书中的文章是从我公开发表的论文中选出来的,选择时考虑了如下几个方面:
(1) 有用,主要是对数学老师的课堂教学实践与研究有实质性帮助,同时对数学教育理论研究有参考价值;
(2) 独到,有独立观点,重点选择那些经过时间考研的、站得住脚的、能较好反映数学育人规律的文章;
(3) 客观,真实反映自己学习、研究和实践数学教育的心路历程,明确表达自己对数学教育改革中各种问题的看法。
以上考虑,主要是希望不要浪费读者的时间和金钱,不要辜负广大数学教师的厚爱。
我把选出的文章分成五个部分:
一 、 数学课程教材
世纪之交,基础教育课程改革风起云涌,我也于 2000 年 8 月从北京师范大学调入人民教育出版社,数学课程、教材的理论与实践自然而然地成为我的“主业”。十几年来,我主持了人教版中学数学教材的研究与编写工作,责任重大,如履薄冰。职责所在,我对数学课程的理论探索,以及中学数学教材的研究、编写与实践检验等不敢懈怠,本部分内容就是这一时期我在数学课程教材方面的主要研究心得,既有宏观的理论探讨,也有具体而微的实践求证。例如,2000 年发表在《课程教材教法》上的“数学课程标准制定中若干问题的思考”,针对当时否定我国数学教育注重双基和数学能力的传统、追捧“建构主义”“大众数学”、照搬美国课标的做法,旗帜鲜明地提出自己的观点,这篇文章很不合时宜,但十几年的课改实践却证明这些观点是站得住的;又如,2007 年发表在《数学通报》上的“为什么用单位圆上点的坐标定义任意角的三角函数”,是对教材中一个具体概念的处理方式的研究,这是针对当时许多老师不理解“人教 A 版”高中数学教材对“任意角三角函数定义”的处理方式而撰写的,这篇文章对广大教师研究教材起了一定的引领作用。
二 、 数学教育心理
这部分文章主要来自于我的硕士论文和博士论文。
硕士论文用当代教育心理学的视角,以数学课堂教学为载体,研究了我国传统的课堂教学核心理论“启发式教学”。显然,启发式教学思想是教育领域的中华优秀传统文化,是至今仍具先进性的教学理论。论文探讨了两个问题:一是从数学学习材料、数学教学目的、数学教学过程及数学学习规律等方面探讨启发式数学教学的基本要求;二是结合“有意义学习理论”“发现式教学”等,讨论了实施启发式教学要关注的几个关键问题,即如何提供学习材料,如何分析学生的认知基础,如何激发学生非认知因素的积极性,如何进行学习策略的指导。非常幸运,北师大数学系的钟善基、丁尔陞、曹才翰、孙瑞清等四位先生都是我的导师。客观地说,在我国数学教育领域,这是一支超豪华导师团队,其整体学术水平无与伦比。在导师们的悉心指导下,再加上我的十年中学数学教师经历,使这篇论文的理论与实践基础都很扎实,得到圈内人的好评。
博士论文研究的是“中学生数学学科自我监控能力的结构、发展和影响因素”问题,这是一项规范的数学能力发展研究,按恩师林崇德先生的评价,这是“严格按照发展心理学专业研究的要求,发挥自己在数学教育上的专业优势,选择自己感兴趣的切入点,对数学能力发展进行了深入研究而完成的博士学位论文,是发展心理学与数学教育学的交叉研究成果,在数学教育的研究方法上具有开创性。既有理论的深刻性,也有数学教学实践的指导性。”我的博士论文纳入张奠宙、李士锜两位先生主编的《数学教育研究前沿》丛书出版后,在选题和研究方法上都对我国数学教育研究起到一定的引领作用。
三 、 数学课堂教学
这里的16篇文章,时间跨度20年,基本反映了我聚焦数学课堂教学开展数学教育研究的足迹。
因为当过十年中学数学教师,所以我对数学课堂教学研究情有独钟。硕士毕业留北师大工作,使我有更多机会接触到国内外先进的数学教育理论文献,对数学课堂教学的研究自然走向理论思考。我的主要兴趣是数学教学设计的理论与实践。1994年在《数学通报》第6期发表“关于课堂教学中设置问题情境的几个问题”一文,从实践层面讨论了问题情境设置的途径和方法。此后,一直坚持不懈,直到2006年在《数学通报》第7期发表“数学课堂教学设计研究”,可以看成是在这个课题上的一个阶段总结。
2006年10月,人教社中数室组织了“中学数学核心概念、思想方法的结构体系及其教学设计的理论研究与实践探索”课题研究,我是课题主持人。这项研究持续了四年,并发展成全国教育科学“十一五”规划2010年度教育部重点课题“中小学数学课程核心内容及其教学的研究”,直到2015年12月底结题。这两项课题使我对课堂教学设计的理论研究进一步深入,所取得的成果在课堂教学实践中得到广泛应用,形成了一系列有较大影响力的案例。其中,最主要的是以启发式教学思想、主体活动理论、建构主义理论等为理论基础,以“理解数学,理解学生,理解教学”为核心思想,围绕中学数学核心概念以及由内容所反映的数学思想方法构建教学设计框架,包含“内容和内容解析”“目标和目标解析”“教学问题诊断分析”“教学支持条件分析”“教学过程设计”“目标检测设计”等六个项目。这一框架经过大量的实践检验,是“实践基础上的理论概括”,体现了课题组的集体智慧,也是我对数学教学的理性思考。本书收入的“注重学生思维参与和感悟的函数概念教学”等,就是在这一理论指导下的代表性成果,涉及函数、几何、统计、向量等,基本涵盖了高中数学的主干内容。另外,根据我国专家型教师的成长经验,为了引导广大教师在实践的基础上加强教学反思,针对教师“不知道如何进行教学反思”的现状,课题组通过专题研究,形成了“数学教学反思的内容与方法(指导意见)”。这一“指导意见”已成为广大一线教师、许多数学教育专业研究生的必读书目。
近几年,我的注意力转向整体观指导下的“单元教学设计”,强调回归数学教育的本来面目,着眼于学生的长期利益,发挥数学的内在力量,挖掘数学内容所蕴含的育人资源,以提高数学素养、发展思维能力、培育理性精神为核心,使学生在掌握数学知识的过程中学会思考,成为善于认识问题、解决问题的人才。我认为这是数学教学中培养学生的创新精神和实践能力的必然要求。这些思考与实践在“让学生在几何学习中学会认识和解决问题的方法”“构建逻辑连贯的学习过程使学生学会思考”等文章中得到了体现。
四 、 数学课改综论
这部分包含两方面内容,一是关于数学课改的理论思考,二是为中国教育学会中学数学教学专业委员会组织的各届“全国中学青年数学教师优秀课观摩与评比活动”所作的总结报告。
总体而言,我对数学课改的理论思考并不是纯思辨性的,所撰写的文章都有扎实的实践基础,大多数是经过数年的教学实际调研,反复提炼、不断总结而成的,而且注重以案例说话,因此这些文章发表后都引起较大反响。例如,发表在《中学数学教学参考》2010 年第 3,4,5 期上的“中学数学课改的十个论题”,原始稿件是 2008 年 12 月在“人教 A 版”高中数学教材年度教学经验交流会上的大会报告,这是在课标教材实施 4 年中进行大量调研基础上形成的。这篇文章澄清了课改中的一些基本问题,发表后被大量引用,有力地引导了广大中学数学教师的教科研和教学实践。“数学教育之取势明道优术”、“数学学习与智慧发展”等文章都是这样形成的。又如,一段时间以来,理论研究者对课程目标与课堂教学目标之间关系的片面解读引起了教学设计与教学实践的混乱,导致一线教师在制定课堂教学目标时无所适从,流行的“三个维度”分列的课堂教学目标,貌似全面且“高大上”,但课堂教学中却无法落实,我针对这一问题撰写了“数学教学目标再思考”等文章。再如,“发挥数学的内在力量为学生谋取长期利益”是针对课改中出现的“去数学化”、教师不注重挖掘数学知识蕴含的育人资源等现象而撰写的。
中国教育学会中学数学教学专业委员会是我国中学数学教师的最高层次学术团体,各省中学数学教研部门都是它的会员单位,“全国中学青年数学教师优秀课观摩与评比活动”以“推动我国中学数学教学研究与改革,提高中学青年数学教师的师德水平、专业水平和教学能力,鼓励中学青年数学教师树立先进的数学教育思想,创新教学模式和教学方法,促进教学过程科学化,提高课堂教学质量,造就一批数学教学名师和学科领军人才”为目标,是学会的标志性品牌活动。参与评比的优秀课是经过层层选拔、由专家教师团队精心打造而成的,因此在一定意义上代表了我国中学数学课堂教学和研究的最高水平。从 2000 年首届高中青年数学教师优秀课评比活动开始,我作为评委参与了每一届活动,并从 2008 年开始全面主持这项活动,每次活动都由我作大会总结暨学术报告。这些报告结合课改发展的新要求,基于评委会对参赛优秀课的分析与评价,比较准确地把握了我国当前数学课堂教学的特点和问题,切实地起到了引领全国中学数学教学改革与发展的作用。本书精选了其中一部分。
这部分以 2015 年在《课程教材教法》第 5 期上发表的“全面深化数学课改的几个关键”收尾,作为与本书开篇的呼应,其中提出的七方面问题:坚持以学生的发展为本的教育理念,明确数学育人的根本目标,优化数学课程、教材和教学结构,全面发挥数学的育人功能,深化课堂教学改革,数学教学设计的精细化,信息技术与数学教学融合的实践与理论,都是数学教育中需要持续研究的关键问题。
五 、编后漫笔集粹
这部分是我为《中小学数学》(高中版)写的“编后漫笔”。这些短文本来也可以按课程、教材、心理、教法等进行分类,但考虑到这组文章具有“随笔”性质,大都是在审阅稿件时受到启发,作为“有感而发”的即时作品,以“流水账”的方式呈现也是有道理的,所以就采取“偷懒”的做法,把 2008——2015 年的所有“编后漫笔”逐篇按时序罗列。
下面再说点题外话,主要说说对数学教育这门学科的粗浅认识。我觉得,数学教育的学科定位一定要强调它的跨学科特征,这一点从国际数学教育大会所列的研究课题中可见一斑;同时要强调它的实践品格,某种意义上,数学教育是一门“应用学科”。这样,对于一个数学教育研究者的要求也就具有“综合性”,既有认知结构的综合性要求,也有课堂教学实践的要求。
数学教育应强调它的数学学科背景,数学教育研究者的数学水平必须过硬,这就像“教好数学的前提是自己先学好数学”的道理一样,否则就不能建立起对数学内容所蕴含的育人力量的敏感性。从一般教育、心理理论泛泛而谈的“数学教育理论”没有多大价值。
如果我们聚焦于数学教育研究的主阵地——数学课堂,那么“数学课程内容的教学表达能力”则是一个关键问题,具体而言就是要具备挖掘数学内容所蕴含的育人资源,为学生设计合情合理的数学学习进程,启发学生独立思考等方面的能力;要在使学生学会抽象数学对象,发现值得研究的问题,构建研究的路径,找到研究方法,获得正确的结论以及在已有基础上发展新知等方面“有招”。
我觉得,归根结蒂,数学教育研究要解决两方面问题,一是数学的学科思想问题,二是学生的思维规律、认知特点问题,而这两方面问题的解决都需要实实在在的数学课堂教学实践作支撑。反思自己的数学教育研究,可以肯定地说,所取得的成绩主要得益于“数学本科+数学教育硕士+教育心理学博士”的学习历程以及十年中学数学教师的经历。
源于对数学教育科学的敬畏之心,感觉自己对她的了解非常有限,谨以《章建跃数学教育随想录》为名,作为我为数学教育研究与实践所尽的绵薄之力。