在某些场合，利用所谓对数求导法求导数比用通常的方法简便些。这种方法是先在
的两边取对数，然后再求出
的导数，即
第一步：由取对数得 
(
)
第二步：再对
求导得 
我们通过下面的例子来说明这种方法。
例1 求 
的导数。
例2 求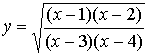
的导数
启示：以上两个例子说明，对数求导法适用于两种情况：
（１）是幂指函数
如例1；
（２）函数是若干个幂指函数的连乘积，如例2．
在这两种情况下,
较易于求导,因此应用对数求导法比较合适.
12月28日的今天，全天监考，很累！
其实还很无聊，所以我就随手翻翻学生放在教室后的那一堆堆书山。翻开一个精致的本子，居然是一整本的心情日记，我很抱歉自己撑着关心学生的幌子看了日记本里面的内容。
很震惊她那华丽的语言，叙述她喜欢一个男生，跟男生交往时冷时热的点滴。“就这么给你开了一个不大不小的玩笑，不经意间晃过，却刻骨铭心” ； “是的，是该忘却的时侯了，昨日的眷念今日的痛苦，以及所有浑浑浊浊翻滚于烈酒中痴狂” ； “我的心太乱害怕爱情的背叛，想哭的我像是一个迷路小孩” ；“爱了，笑了，伤了，痛了，一切都算了吧…”
我不认识这个孩子，我也不会了解到高中时候的她以及她的“爱情”，只是她的那些语言让我知道明白她很纠结。只有祝福她，祝福她快乐健康，用青春论证爱情的纯洁！
送给她一个FLASH，一直保存在我电脑里/可能网上也找不着的mv《求爱复刻版》！
明天9月1号，我和周蒲就正式开学上课了（我中学老师，她大学老师）。
暑假好像很长，长得我都忘记了很多好玩和不好玩的事情；暑期好像也很短，短的好像7月1日放假就在昨天。不管怎样，一转眼，日子过去，又是新的一学年！
别的也不多说，把以前做好的一个flash放在此处，回忆过去美好的同时，也祝愿以后的日子里我们能永远开心快乐！（烦请看到此处的朋友写下你的祝福，Ann & Tgg也祝你能健康快乐，呵呵）
向大家推荐这个软件。
关于软件的使用感受，亚选（关注E-learning,大家可以看看他的博客）介绍的比较好，直接引用。
iSpring Free是一款免费的PPT转换flash工 具，可以轻松地将PPT演示文档转换为对Web友好的Flash影片格式，转换的同时将会保留原有的可视化与动画效果，而Flash格式的最大特点是体积 小巧、易于分发，兼容所有的操作系统和浏览器等。而这一切都是免费的，虽然收费的Pro版能自定义更多的选项，Free版的对我们日常情况也已经够用了！
iSpring 是以PowerPoint插件的形式工作的，下载解压后先运行 !)iSpringFree_绿化工具.exe，选择 安装 后会自动添加插件，再打开PowerPoint就能看到了；iSpring Free 5.0（v5.0.0 Build 2834）已完全兼 容Office 2010及Windows 7。
我在PowerPoint 2003/2007/2010下测试通过，转换效果很是不错，与原有PPT文档相差无几，只是对一些图像质量有所下降，应是压缩的缘故！ 若绿色版有问题，请使用官方安装版。
* 支持PowerPoint 2000/XP/2003/2007/2010；
* 支持超链接和动作按钮；
* 超过180中的PowerPoint动画效果；
* 支持所有的PowerPoint幻灯片切换效果；
* 单击即可轻松转换；
* 嵌入式的音乐、音频支持；
* 自动同步动画与声音；
* 嵌入视频剪辑与Flash影片；
* 基于Flash的播放器；
* 将YouTube视频插入到幻 灯片中。
你可以直接点击 Quick Publish 直接发布为Flash影片，iSpring会以默认参数发布，生成SWF与HTML文件，同时保存到文档文档目录；需要自定义的话请点击 Publish 会跳出选项对话框，再设置相关选项即可。下载请移步这里http://www.portablesoft.cn/ispring-free/
大师版的http://www.portablesoft.cn/ispring-presenter/
让所有80后“内牛满面”的MV。
“Li Lei和Han Meimei没在一起啊？”最近，一些“80后”们发现，曾是他们初中英语教材中两个主要人物的“Li Lei”和“Han Meimei”被一套新的英语教材沿用。但令人惊讶的是，新教材中的Li Lei和Han Meimei已不再是小朋友，而是跟着80后们一起步入了青年时代。Han Meimei更嫁作了他人妇。